Discussions:
Hacker News (63 points, 8 commentaires), Reddit r/programming (312 points, 37 commentaires)
Traductions:
Anglais
Espagnol
Mise à jour : La 2ᵉ partie est maintenant en ligne : Regard visuel et interactif sur les mathématiques de base des réseaux neuronaux
Motivation
Je ne suis pas un expert de l'apprentissage automatisé. Je suis ingénieur logiciel de formation et j'ai eu peu d'interactions avec l'IA. J'ai toujours voulu plonger plus profondément dans le machine learning, mais sans jamais trouver mon "entrée". C'est pourquoi lorsque Google a publié TensorFlow en Open Source en , j'ai été super excité et j'ai su que c'était le moment de m'y mettre et de commencer le long trajet de l'apprentissage. Sans vouloir dramatiser, pour moi, c'était comme être une sorte de Prométhée apportant le feu à l'humanité depuis le Mont Olympe de l'apprentissage automatique. Je me souvenais encore que tout le domaine du Big Data et des technologies comme Hadoop avaient été énormément accélérés lorsque les chercheurs de Google avaient publié leur article sur Map-Reduce. Cette fois ce n'était pas un article – c'est le logiciel-même qu'ils utilisent en interne, après des années et des années d'évolution.
J'ai donc commencé à apprendre ce que je pouvais sur les bases du sujet, et ai pu constater le besoin de ressources plus accessibles pour des personnes n'ayant aucune expérience dans le domaine. Ceci est mon effort dans ce sens.
Commencez ici
Commençons par un exemple simple. Disons que vous aidez une amie qui veut acheter une maison. On lui a proposé 400 000$ pour une maison de 2000 pieds² (185 m²). Est-ce un bon prix ou non ?
Ce n'est pas facile à dire sans données de référence. Vous demandez donc à des amis ayant acheté une maison dans la même zone, ce qui vous mène à 3 points de données :
| Surface (pieds²) () | Prix () |
|---|---|
| 2104 | 399 900 |
| 1600 | 329 900 |
| 2400 | 369 000 |
Personnellement, mon premier instinct serait de prendre le prix moyen par pied². Cela revient à 180 $ par pied².
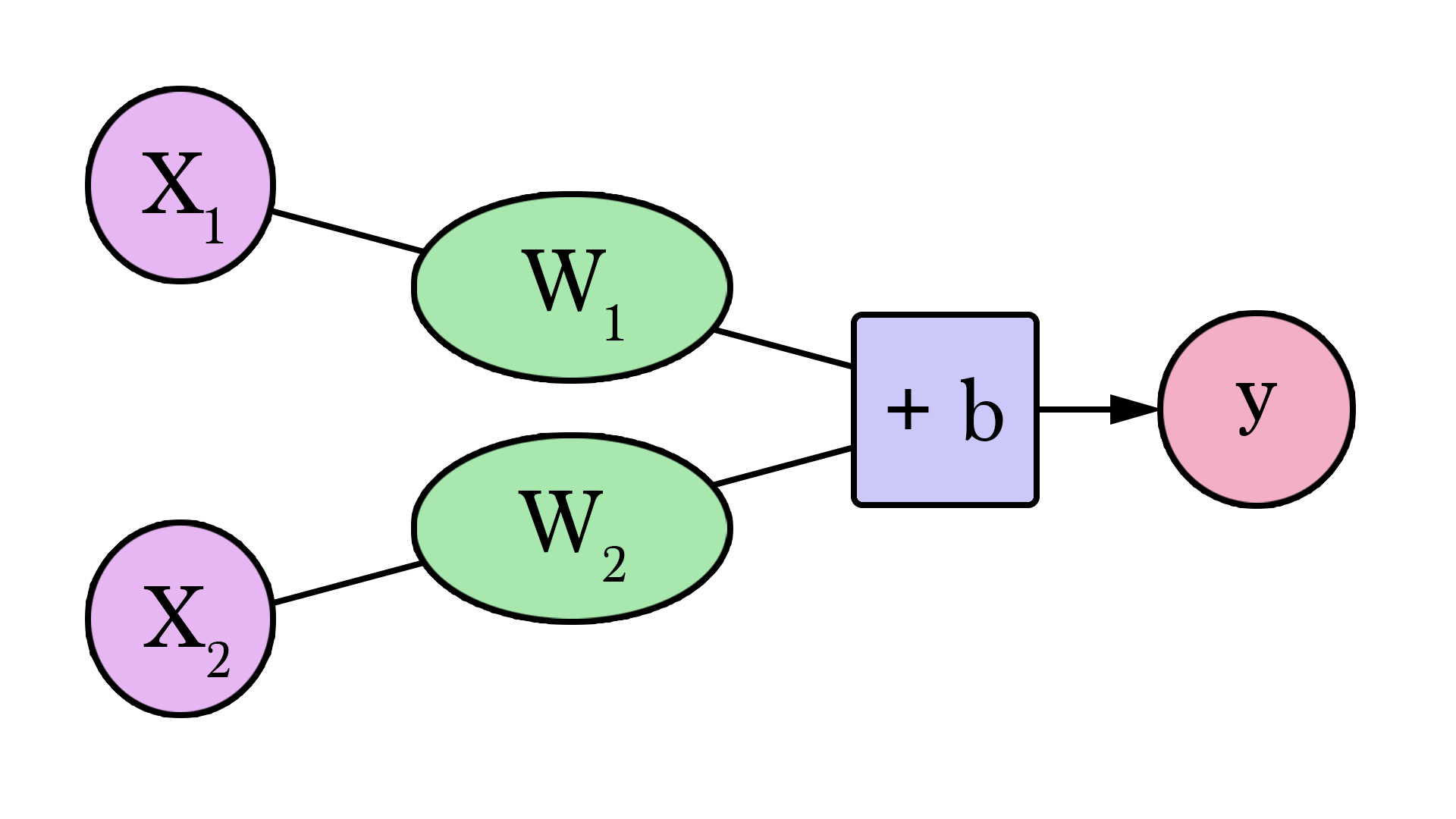
Bienvenue dans votre premier réseau neuronal ! Bon ce n'est pas encore du niveau de Siri, mais vous en connaissez maintenant une brique fondamentale. Et elle ressemble à ceci :
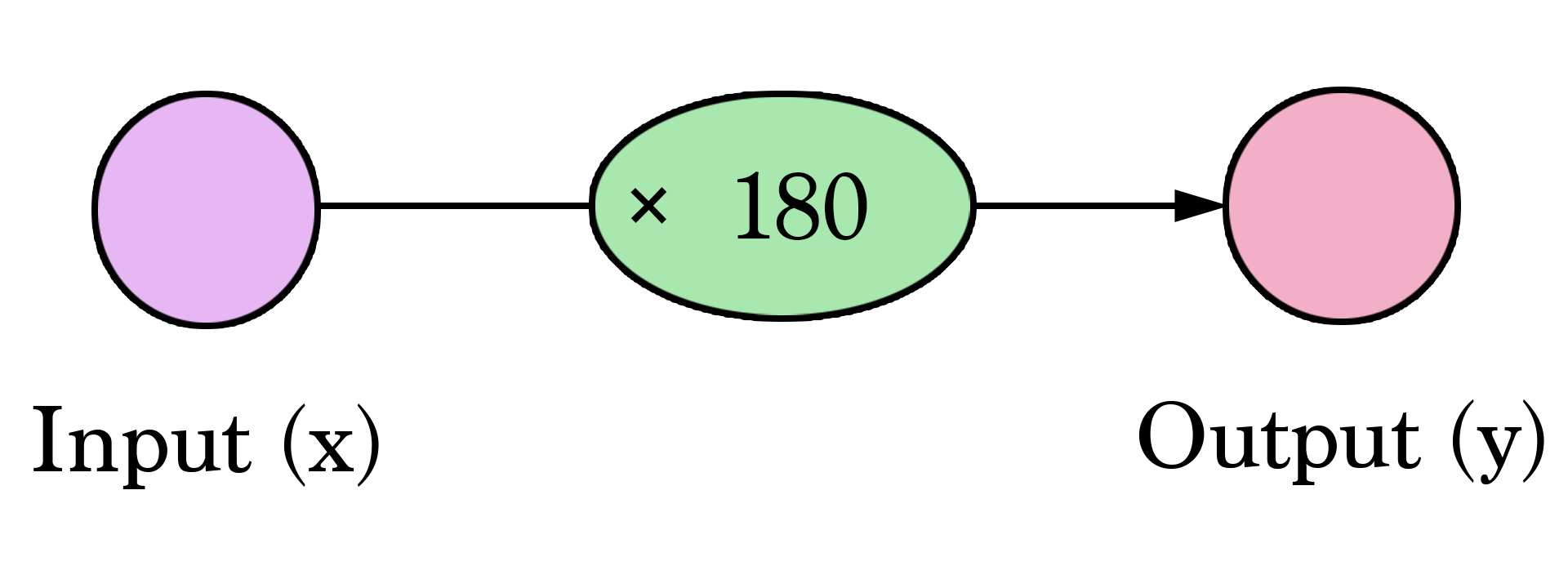
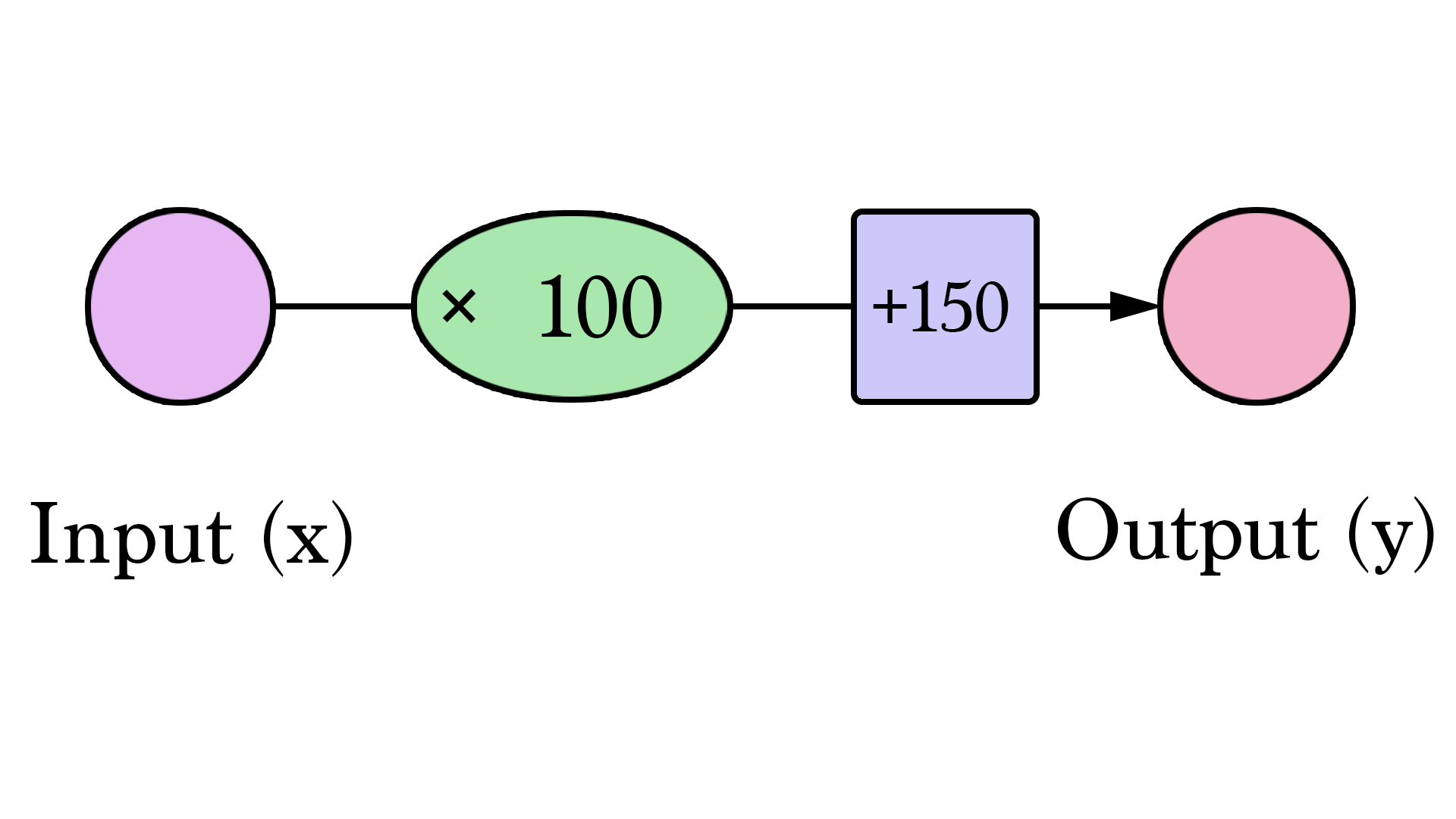
Des diagrammes comme celui-ci vous montrent la structure du réseau et comment il calcule une prédiction. Le calcul commence au noeud d'entrée à gauche. La valeur d'entrée va à droite. Elle y est multipliée par le poids et le résultat devient notre sortie.
Multiplier 2000 pieds² par 180 nous donne 360 000 $. Cela se résume à ça à ce niveau. Calculer la prédiction est une simple multiplication. Mais avant cela, nous avons eu besoin de réfléchir au poids par lequel nous allions multiplier. Ici nous avons commencé par une moyenne ; plus tard nous examinerons de meilleurs algorithmes capables de supporter plus d'entrées et des modèles plus compliqués. Trouver le poids est notre étape d'"entraînement". Donc chaque fois que vous entendez que quelqu'un "entraîne" un réseau de neurones, cela veut juste dire trouver les poids que nous utilisons pour calculer la prédiction.
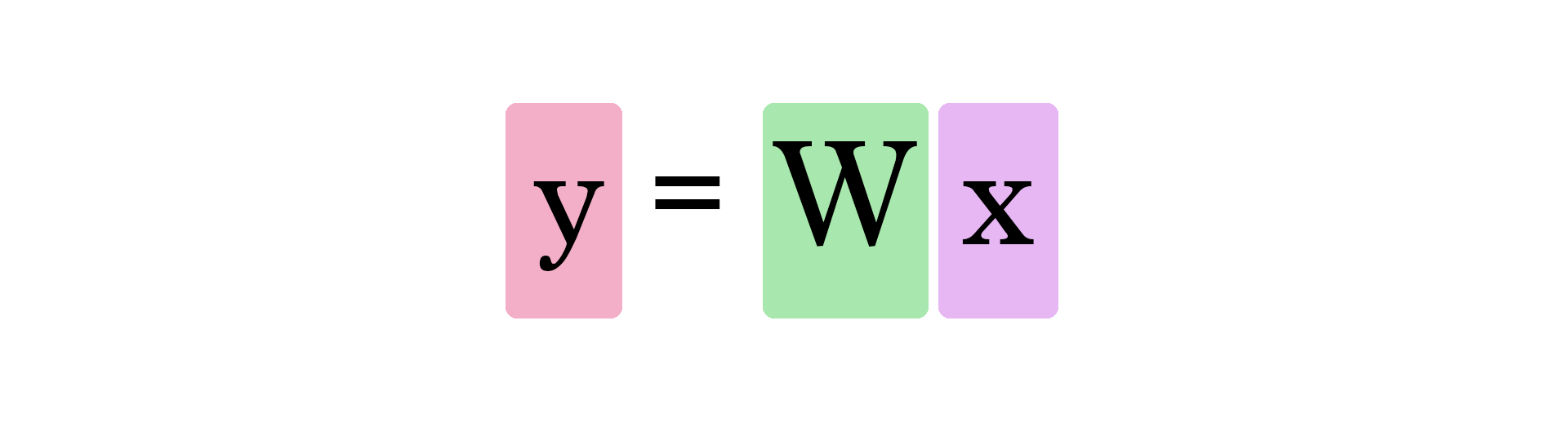
Ceci une forme de prédiction. Il s'agit d'un modèle prédictif simple qui prend une entrée, effectue un calcul, et fournit une sortie (la sortie pouvant être des valeurs continues, la terme technique pour ce que nous avons serait un "modèle de régression").
Essayons de visualiser ce processus (à des fins de simplicité, changeons notre unité de prix de 1 $ à 1000 $. Notre poids est maintenant de 0,180 plutôt que 180):
Plus dur, meilleur, plus rapide, plus solide
Pouvons-nous faire mieux qu'estimer le prix sur la base de la moyenne de nos points de données ? Essayons. Commençons par définir ce que veux dire faire mieux dans ce scénario. Si nous appliquons notre modèle aux 3 points de données dont nous disposons, quelle qualité fournirait-il ?
Cela fait beaucoup de jaune. Le jaune, c'est mal. Le jaune, c'est de l'erreur. Nous voulons réduire le jaune autant que possible.
| Surface () | Prix ($1000) () | Prédiction () | -y | (-)² |
|---|---|---|---|---|
| 2104 | 399,9 | 379 | 21 | 449 |
| 1600 | 329,9 | 288 | 42 | 1756 |
| 2400 | 369 | 432 | -63 | 3969 |
| Moyenne : | 2058 | |||
Ici on peut voir la valeur du prix réel, la valeur du prix prédite et la différence entre elles. Nous aurons alors besoin de faire la moyenne de ces différence afin d'avoir un nombre qui nous indique la quantité d'erreur dans ce modèle prédictif. Le problème est que la 3ᵉ ligne a une valeur de -63. Nous devons traiter cette valeur négative si nous voulons utiliser la différence entre prédiction et prix comme instrument de mesure de l'erreur. C'est une des raisons pour lesquelles nous introduisons une colonne supplémentaire qui montre l'erreur au carré, éliminant ainsi la valeur négative.
C'est maintenant notre définition de faire mieux – un meilleur modèle est un modèle qui a moins d'erreur. L'erreur est mesurée comme la moyenne des erreurs pour chaque point de notre ensemble de données. Pour chaque point, l'erreur est mesurée par la différence entre la valeur réelle et la valeur prédite, élevée à la puissance 2. On appelle ça l'erreur quadratique moyenne. L'utiliser comme guide pour entraîner notre modèle en fait notre fonction de coût (ou encore fonction de perte).
Maintenant que nous avons défini notre instrument de mesure de ce qui fait un meilleur modèle, expérimentons quelques autres valeurs de poids et comparons-les avec notre choix de la moyenne :
Nos lignes peuvent mieux approcher nos valeurs maintenant que nous avons cette valeur ajoutée à la formule linéaire. Dans ce contexte, nous l'appelons un "biais". Cela fait ressembler notre réseau de neurones à ceci :
Nous pouvons le généraliser en disant qu'un réseau de neurones avec 1 entrée et 1 sortie (attention spoiler : et aucune couche cachée) ressemble à ceci :
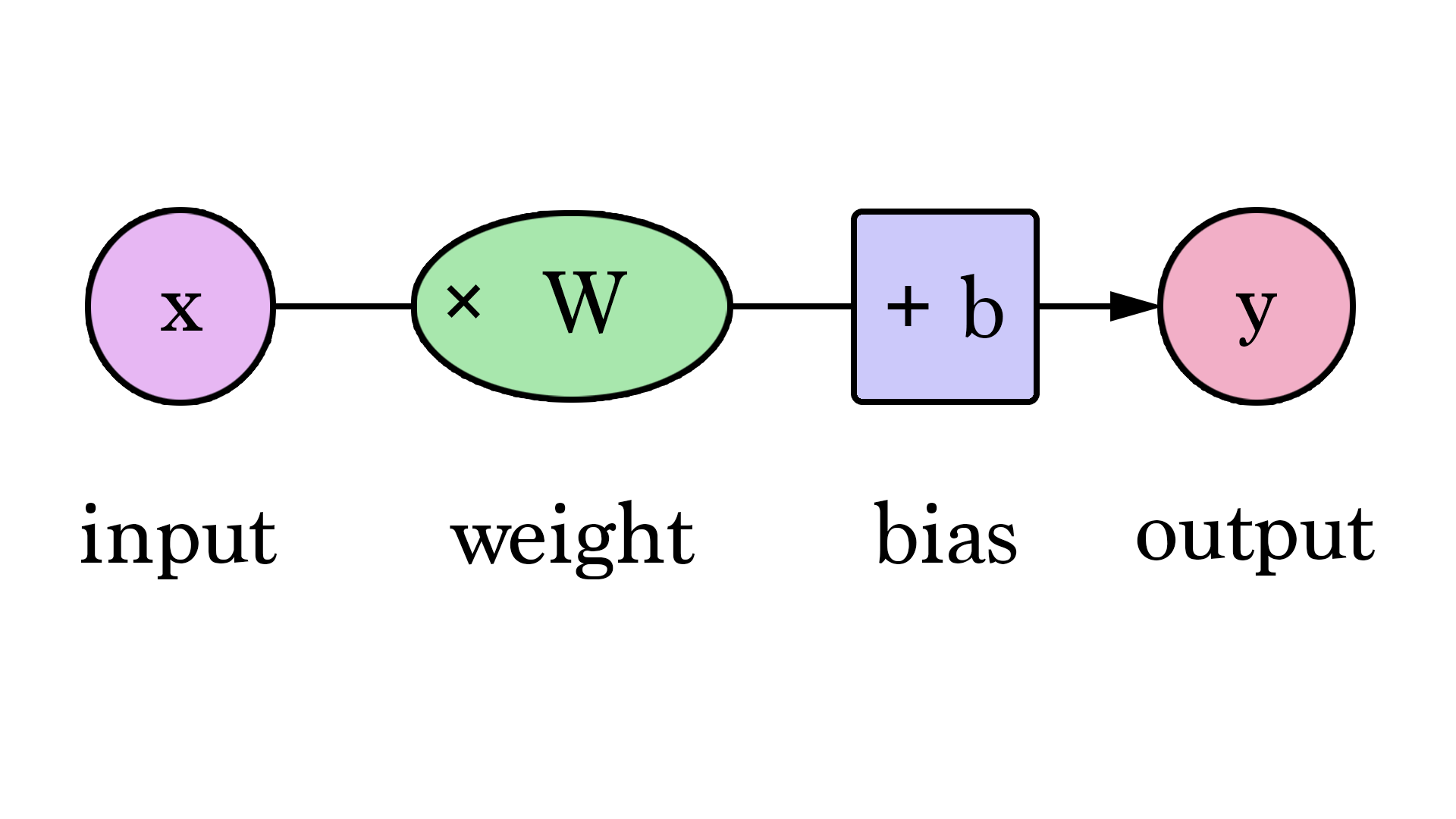
Dans ce graphique, et sont des valeurs que nous trouvons au cours de l'entraînement. est l'entrée que nous branchons dans la formule (surface en pieds² dans notre exemple). Y est le prix prédit.
Le calcul d'une prédiction utilise maintenant cette formule :
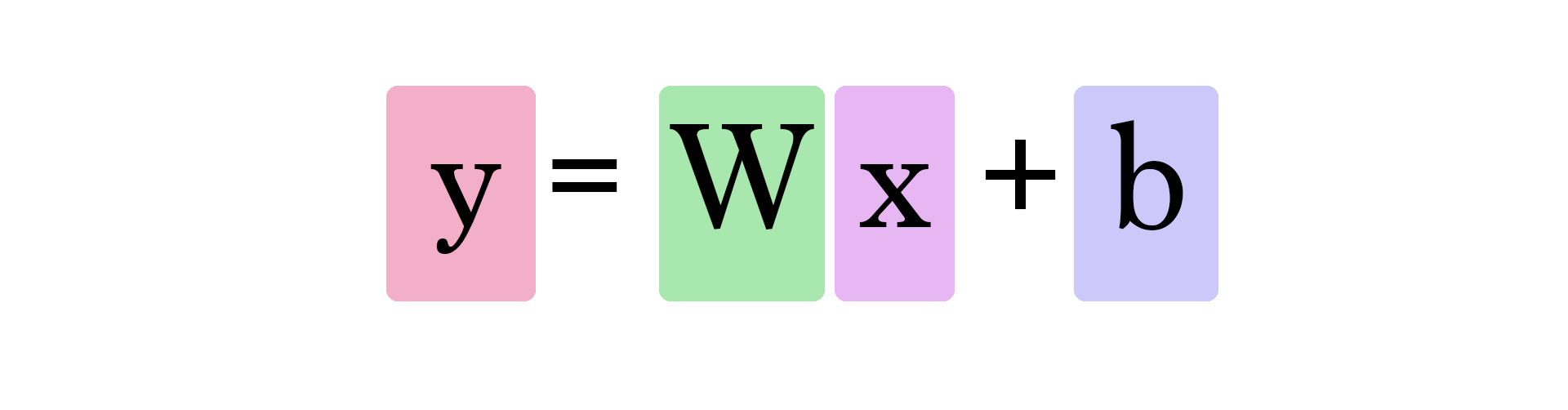
Notre modèle actuel calcule donc les prédictions en branchant la surface de la maison comme dans cette formule :
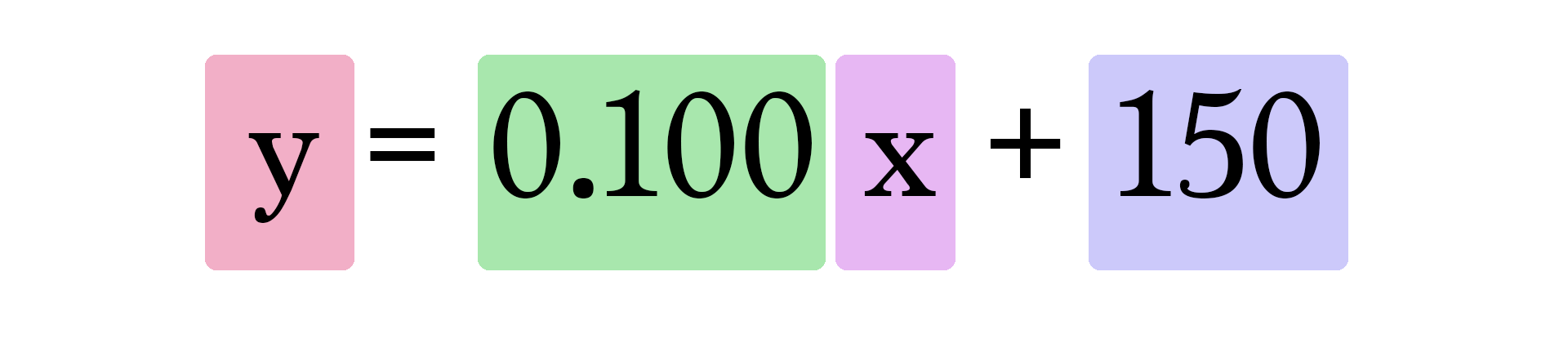
Entraînez votre dragon
Que diriez-vous d'essayer d'entraîner notre réseau de neurones d'exemple ? Minimisez la fonction de coût en ajustant les curseurs de poids et de biais. Pouvez-vous obtenir une erreur en-dessous de 799 ?
| Erreur | ||
| 0 | ||
| 0 | ||
Automatisation
Félicitations pour avoir entraîné manuellement votre premier réseau de neurones ! Regardons maintenant comment automatiser ce processus d'entraînement. Ci-dessous se trouve un autre exemple avec une fonctionnalité supplémentaire d'auto-pilotage. Il s'agit des boutons Itération DG. Ils utilisent un algorithme appelé "Descente de Gradient" pour essayer d'itérer vers les valeurs correctes de poids et biais corrects qui minimise la fonction de coût.
| Erreur | ||
| 0 | ||
| 0 | ||
Les 2 nouveaux graphiques sont là pour vous aider à suivre les valeurs d'erreur à mesure que vous bidouillez les paramètres (poids et biais) du modèle. Il est important de garder une trace de l'erreur car le processus d'entraînement vise à réduire cette erreur autant que possible.
Comment la descente de gradient sait-elle où devrait être sa prochaine itération ? Par calcul : en connaissant la fonction que l'on minimise (notre fonction de coût, la moyenne de pour l'ensemble de nos points de données), et en connaissant ses entrées à un moment donné (des poids et biais donnés), les dérivées de la fonction de coût nous indiquent dans quelle direction pousser et afin de minimiser l'erreur.
Vous en apprendrez plus sur la descente de gradient et comment l'utiliser pour calculer les nouveaux poids & biais dans les premiers exposés du cours sur l'apprentissage automatique de Coursera.
Puis il y en eut deux
La taille de la maison est-elle la seule variable influant sur son coût ? À l'évidence il existe d'autres facteurs. Ajoutons une autre variable et voyons comment nous pouvons y ajuster notre réseau de neurones.
Disons que notre amie a fait un peu de recherche et a trouvé pas mal de points de données supplémentaires. Elle a aussi trouvé combien de salles de bain avait chaque maison :
| Surface (pieds²) () | Salles de bain () | Prix () |
|---|---|---|
| 2104 | 3 | 399 900 |
| 1600 | 3 | 329 900 |
| 2400 | 3 | 369 000 |
| 1416 | 2 | 232 000 |
| 3000 | 4 | 539 900 |
| 1985 | 4 | 299 900 |
| 1534 | 3 | 314 900 |
| 1427 | 3 | 198 999 |
| 1380 | 3 | 212 000 |
| 1494 | 3 | 242 500 |
Notre réseau de neurones à 2 variables ressemble à ceci :

Nous devons maintenant trouver 2 poids (1 pour chaque entrée) et 1 biais pour créer notre nouveau modèle.
Calculer ressemble à ceci :
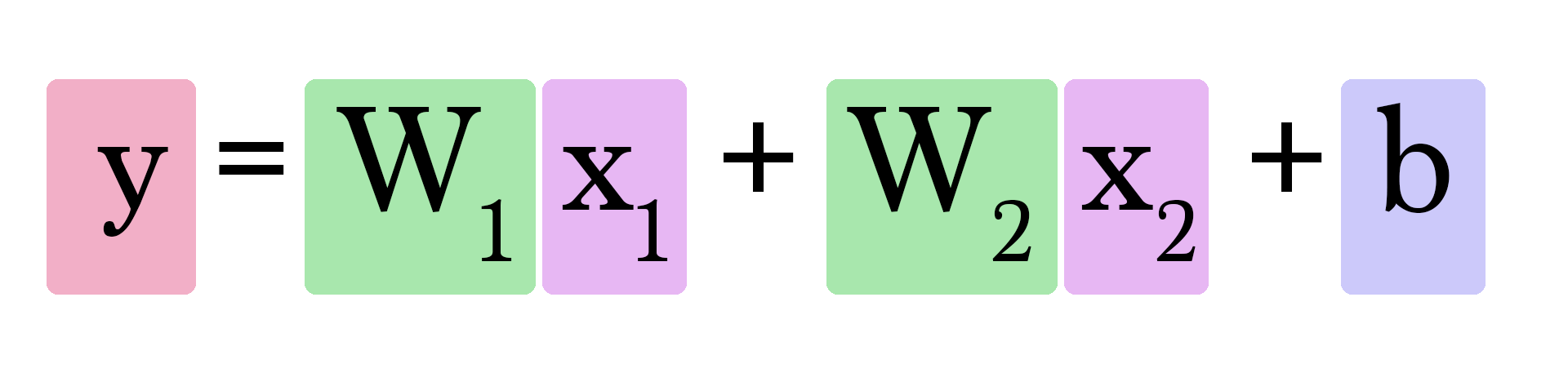
Mais comment trouvons-nous et ? C'est un peu plus compliqué que lorsque nous n'avions à nous soucier que d'une seule valeur de poids. Dans quelle mesure avoir une salle de brain supplémentaire affecte la manière dont nous prédisons la valeur d'une maison ?
Essayez de trouver les bons poids et biais. Vous allez commencer ici à voir la complexité dans laquelle nous commençons à plonger à mesure que le nombre de nos entrées augmente. Nous commençons à avoir du mal à créer des formes en 2D simples qui nous permettent de visualiser le modèle d'un coup d'œil. Au lieu de cela, nous allons devoir nous reposer principalement sur la manière dont la valeur d'erreur évolue lorsque nous ajustons les paramètres de notre modèle.
| Erreur | ||
| 0 | ||
| 0 | ||
| 0 | ||
Notre fidèle descente de gradient nous aide encore une fois. Elle reste utile pour nous aider à trouver les bons poids et biais.
Paramètres
Maintenant que vous avez vu des réseaux de neurones avec 1 ou 2 paramètres, vous pouvez deviner comment ajouter des paramètres et les utiliser pour calculer vos predictions. Le nombre de poids continuera d'augmenter, et notre implémentation de la descente de gradient devra être ajustée à chaque fois que l'on ajoute un paramètre, afin qu'elle puisse mettre à jour les nouveaux poids associés aux nouveaux paramètres.
Il est important de noter ici que l'on n'alimente pas aveuglément le réseau avec tout ce que l'on sait de nos exemples. Nous devons être sélectifs quant aux paramètres que nous fournissons au modèle. La sélection et le traitement des paramètres et une discipline à part entière qui a son propre lot de considérations et bonnes practiques. Si vous souhaitez voir un exemple du processus consistant à examiner un ensemble de données dans le but de choisir quelles caractéristiques fournir en entrée d'un modèle de prédiction, regardez Un voyage sur le Titanic. Il s'agit d'un bloc-notes où Omar EL Gabry relate son processus de résolution du défi Titanic de Kaggle. Kaggle publie la liste des passagers du Titanic incluant des données comme les nom, sexe, âge, cabine et si la personne a survécu ou non. Le défi consiste à élaborer un modèle capable de prédire si une personne a survécu ou non étant données leurs autres informations.
Classement
Continuons à affiner notre exemple. Supposons que notre amie nous donne une liste de maisons. Cette fois, elle a indiqué lesquelles selon elle ont une bonne taille et le nombre de salles de bains :
| Surface (pieds²) () | Salles de bain () | Libellé () |
|---|---|---|
| 2104 | 3 | Bon |
| 1600 | 3 | Bon |
| 2400 | 3 | Bon |
| 1416 | 2 | Mauvais |
| 3000 | 4 | Mauvais |
| 1985 | 4 | Bon |
| 1534 | 3 | Mauvais |
| 1427 | 3 | Bon |
| 1380 | 3 | Bon |
| 1494 | 3 | Bon |
Elle vous demande d'utiliser ceci pour créer un modèle capable de prédire si elle aimera une maison ou non, étant donnés sa taille et son nombre de salles de bain. Vous utiliserez la liste ci-dessus pour élaborer le modèle, puis elle utilisera le modèle pour classer nombre d'autres maisons. Un autre changement dans le processus est qu'elle a une autre liste de 10 maisons qu'elle a libellées, mais qu'elle ne vous montre pas. Cette autre list sera utilisée pour évaluer votre modèle une fois que vous l'aurez entraîné – essayant ainsi de s'assurer que votre modèle capte les conditions qui font qu'elle aime les caractéristiques d'une maison.
Les réseaux de neurones sur lesquels nous nous sommes exercés jusqu'à maintenant faisaient tous des "regressions" – ils calculaient et sortaient une valeur "continue" (la sortie peut être 4, ou 100,6 ou 2143,342343). En pratique, cependant, les réseaux de neurones sont plus souvent utilisés dans les problèmes de type "classement". Dans ces problèmes, la sortie du réseau de neurones doit faire partie d'un ensemble de valeurs discrètes (ou "classes") comme "Bon" ou "Mauvais". En pratique, nous aurons un modèle qui dira être à 75% sûr qu'un choix de maison est "Bon" plutôt que juste dire "bon" ou "mauvais".

Une manière de transformer le réseau que nous avons vu en réseau de classement est de lui faire sortir 2 valeurs – une pour chaque classe (nos classes étant maintenant "bon" et "mauvais"). Nous devons alors faire passer ces valeurs à travers une opération appelée "softmax". Le sortie d'un softmax est la probabilité de chaque classe. Par exemple, disons que la couche du réseau sort 2 pour "bon" et 4 pour "mauvais" ; si nous entrons [2, 4] dans le softmax, il retournera [0,11, 0,88] en sortie. Ce qui traduit les valeurs pour dire que le réseau est à 88% sûr que la valeur entrée est "mauvaise" et que notre amie n'aimera pas cette maison.
Softmax prend un tableau et sort un tableau de la même taille. Notez que les sorties sont toutes positives et que leur addition donne 1 – ce qui est pratique lorsque l'on sort une valeur de probabilité. Notez aussi que même si 4 est le double de 2, sa probabilité n'est pas seulement le double, mais est de 8 fois celle de 2. Il s'agit d'une propriété utile qui exagère la différence en sortie, améliorant ainsi notre processus d'entraînement.
| sortie | |
|---|---|
| softmax([ 1 ]) | [ 1 ] |
| softmax([ 1, 1 ]) | [ 0.5, 0.5 ] |
| softmax([ 0, 1 ]) | [ 0.26, 0.73 ] |
| softmax([ 2, 4 ]) | [ 0.11, 0.88 ] |
| softmax([ 5, 10 ]) | [ 0.007, 0.993 ] |
| softmax([ -1, 0, 1 ]) | [ 0.09, 0.24, 0.66 ] |
| softmax([ 1, 2, 4 ]) | [ 0.04, 0.11, 0.84 ] |
Comme nous le voyons dans les 2 dernières lignes, softmax s'étend à n'importe quel nombre d'entrées. Donc si notre amie ajoute un 3ᵉ libellé (disons “Bon, mais je devrai louer une chambre sur airbnb"), softmax s'adapte à ce changement.
Prenez un moment pour explorer la forme du réseau lorsque vous faites varier le nombre de paramètres ( etc) (qui peuvent être la surface, le nombre de salles de bain, le prix, la proximité de l'école/du travail… etc) et faites varier le nombre de classes ( etc) (qui peuvent être "trop cher", "bonne affaire", "bien si je loue sur airbnb", "trop petit") :
Vous trouverez un exemple de comment créer et entraîner ce réseau avec TensorFlow dans ce bloc-notes que j'ai créé pour accompagner cet article.
Vraie motivation
Si vous êtes arrivé(e) jusqu'ici, je dois vous révéler une autre motivation qui m'a incité à écrire cet article. Cet article vise à être une introduction encore plus accessible aux didacticiels de TensorFlow. Si vous commencer à travailler MNIST pour débutants en ML maintenant, et tombez sur ce graphique :
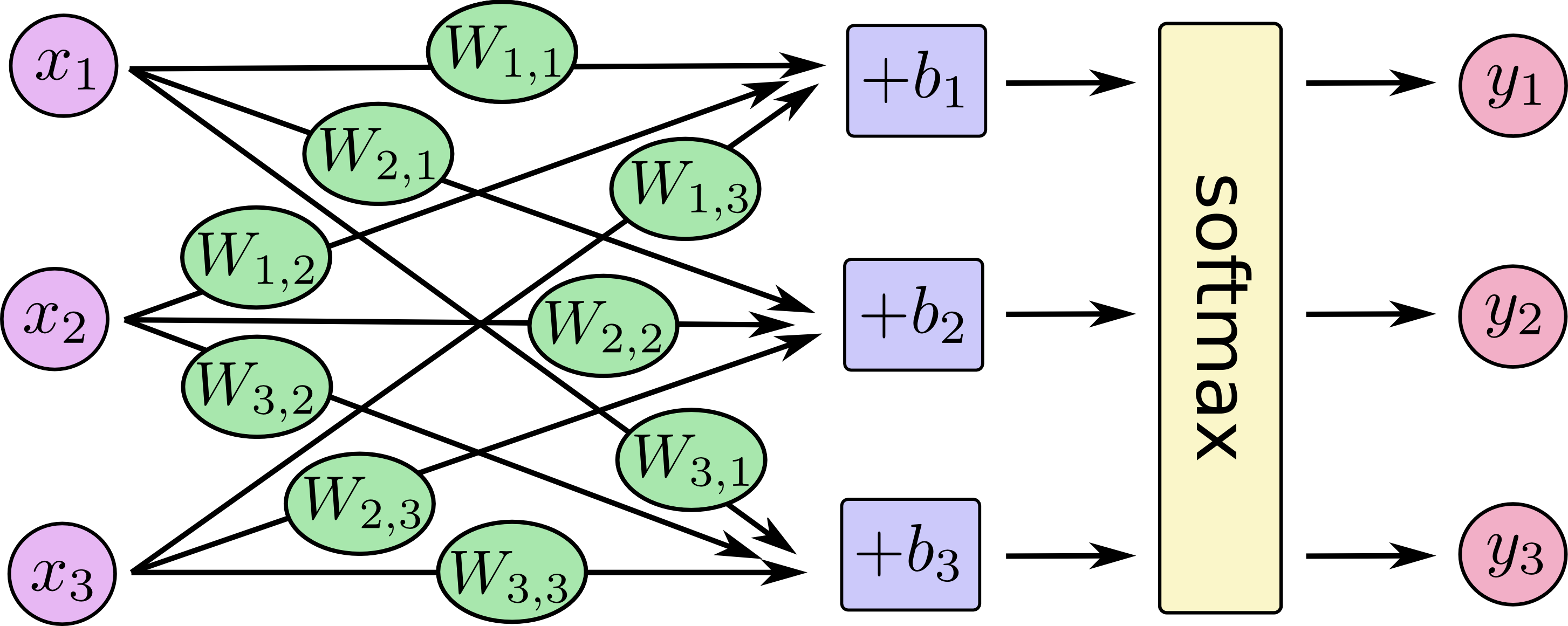
J'espère que vous vous sentez prêt et que vous comprenez maintenant ce système et comment il fonctionne. Si vous souhaitez commencer à bricoler du code, n'hésitez pas à le récupérer du didacticiel de l'intro et apprendre à un réseaux de neurones à reconnaître des chiffres manuscripts.
Vous devriez aussi poursuivre votre formation en apprendre les sous-jacents théoriques et mathématiques des concepts que nous avons discutés ici. Parmi les bonnes questions à poser maintenant se trouvent :
- Quels autres types de fonctions de coût existent ? Quelles sont les plus adaptées à quelles applications ?
- Quel est l'algorithme pour calculer concrètement les nouveaux poids en utilisant la descente de gradient ?
- Quelles sont les applications de l'apprentissage automatique dans les domaines que vous connaissez déjà ? Quelle nouvelle magie pouvez-vous insuffler en mixant ce pouvoir avec d'autres dans votre livre de sorts ?
Parmi de très bonnes ressources pour apprendre on trouve :
- Le cours sur apprentissage automatique de Coursera par Andrew Ng. C'est celui avec lequel j'ai commencé. Il commence avec la regression puis passe au classement et aux réseaux neuronaux.
- Réseaux de neurones pour apprentissage automatique de Coursera par Geoffrey Hinton. Plus centré sur les réseaux de neurones et leurs applications visuelles.
- CS231n: Convolutional Neural Networks for Visual Recognition de Stanford, par Andrej Karpathy. Il est intéressant de voir des concepts avancés et l'état de l'art dans la reconnaissance visuelle en utilisant des réseaux de neurones profonds.
- Le Neural Network Zoo est une très bonne ressource pour en apprendre plus sur les différents types de réseaux de neurones.
Remerciements
Merci à Yasmine Alfouzan, Ammar Alammar, Khalid Alnuaim, Fahad Alhazmi, Mazen Melibari, and Hadeel Al-Negheimish pour leur aide à revoir les versions précédentes de cet article.
Merci de me contacter sur Twitter pour toutes corrections ou retours.

Cet article est publié sous licence Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Exemple d'attribution :
Alammar, Jay (2018). The Illustrated Transformer [Blog post]. Récupéré de https://jalammar.github.io/illustrated-transformer/
Note : Si vous traduisez un de mes articles, faites-le moi savoir pour que je puisse ajouter un lien vers votre traduction de l'article d'origine. Mon email est dans la page À propos.