Derivative.
Motivation
Déterminer la pente d'une fonction en un point.
Analyse
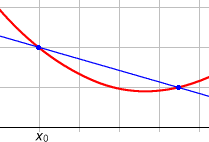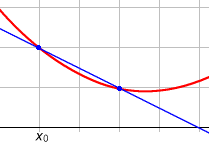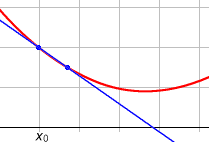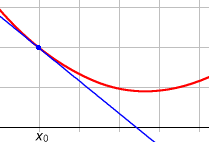
On considère que la pente est donnée par la tangente (plus précisément le coefficient directeur de cette tangente) à la fonction en un point.
On note `f'(x)` ou `(df)/(dx)` ou `(δf)/(δx)` la fonction dérivée de `f(x)` (où `dx` et `df` représentent des accroissement infinitésimaux de `x` et `f(x + dx)`).
Plusieurs variables
Si la fonction implique plusieurs variables/dimensions `x_1, x_2, ..., x_n`, la dérivée est la somme des dérivées dans chaque variable/dimension :
`df = (δf)/(δx_1) + (δf)/(δx_2) + ... + (δf)/(δx_n)`
de sorte que l'on peut calculer chacune de ces dérivées partielles indépendamment (comme si les autres variables étaient constantes).
Conception

Pour trouver la tangente, on la définit comme passant par 2 points de la fonction (espacés d'un petit écart `h` en abscisse), et l'on chercher à trouver quelle sera la pente lorsque ces points seront rapprochés au maximum (i .e. lorsque `h` tend vers 0).
Exemples
Des exemples de fonctions dérivées sont :
| Fonction `f =` | Graphique | Fonction dérivée `f'=` | Explication de la dérivée |
|---|---|---|---|
| constante | 0 | La pente d'une ordonnée constante (ligne horizontale) est nulle | |
| `x` | 1 | `y = x` est une diagonale montant de `h` quand `x` augmente de `h` | |
| `ax + b` | `a ` | La pente de la droite est `a`, `b` est juste la position en `x = 0`, i.e. l'intersection avec l'axe des ordonnées | |
| `x^n` | `nx^(n-1)` |
Des exemples d'utilisation des dérivées sont :
- Recherche du minimum d'une fonction => recherche du point où sa dérivée est nulle (puisque cela veut dire qu'elle est descendue puis remontée).
- Descente de gradient => pente de descente