Les observations des gendarmes von Montigny et Nicoll (figure 1) montrent que les "phares" peuvent également émettre des "faisceaux lumineux". Nous savons qu'ils ont des propriétés très spéciales, que nous avons attribuées à une radiation qui rendrait l'air lumineux. Quelle radiation ? Il faudrait qu'elle ionise l'air et qu'il y ait un lien entre le mécanisme de l'émission des faisceaux lumineux et le système de guidage auxiliaire.
Admettons qu'il y ait seulement un champ électrique E perpendiculaire à la surface du phare et pas de champ magnétique (ou pas de champ magnétique oscillant à la fréquence adéquate). La fréquence et l'amplitude du champ électrique peuvent être modifiées si l'on veut, mais nous supposons que l'amplitude des oscillations est assez grande pour provoquer une ionisation de l'air. Les particules chargées seraient alors mises en oscillation suivant la direction du champ électrique. Si ces oscillations se communiquent de proche en proche, on obtient une "onde de plasma".
Il y a 2 types d'oscillations de plasma possibles, suivant que les particules qui oscillent sont des électrons ou des ions. Cela dépend uniquement de la fréquence de ces oscillations. En effet, les électrons ont une masse tellement petite, qu'ils oscillent facilement à haute fréquence, tandis que les ions, plus lourds, n'arrivent pas à suivre. Si les électrons se déplacent de manière collective, il en résulte une perturbation de la neutralité électrique. On crée donc un champ électrique qui tend à ramener les électrons à leur position d'équilibre, mais ils dépassent celle-ci. Ils vont donc osciller comme le fait un pendule, avec une fréquence propre bien déterminée. Elle se situe dans le domaine des gigahertz (micro-ondes).
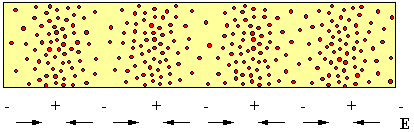
La situation est très différente pour des fréquences plus basses. Pour garder notre raisonnement aussi simple que possible, nous nous limitons au cas d'un plasma constitué d'électrons et d'ions positifs (sans ions négatifs). Dans son état d'équilibre, le plasma est tel que les particules positives et négatives sont réparties statistiquement de manière uniforme, mais on peut créer des mouvements collectifs des ions. Pour aider notre imagination, nous représentons les ions positifs par des cercles noirs (figure 20). A un instant donné, ils sont plus concentrés dans des bandes équidistantes, tandis que la distribution des électrons est représentée par un fond gris. A cause de leur petite masse, les électrons se meuvent très rapidement et ils subissant beaucoup de collisions. Ils sont donc en équilibre thermique, mais à une température électronique Te très supérieure à la température T du plasma, déterminée par l'agitation thermique des ions. On peut avoir une température électronique de l'ordre de 1000 K, tandis que la température T du plasma reste de l'ordre de 300 K.
Si nous admettons que les électrons sont distribués de manière uniforme, le plasma sera positif dans les couches où les ions positifs se sont rassemblés et négatif entre ces couches. Il en résulte qu'il y aura un champ électrique E, avec des orientations alternées. Puisque les ions oscillent, le champ électrique oscille également. Ces oscillations sont en général un peu déphasées quand on considère des oscillations voisines. Cela veut dire qu'on obtient une onde de plasma ionique qui se propage à une certaine vitesse. Cette vitesse dépend de la longueur d'onde qui détermine la périodicité spatiale de la répartition des ions (figure 20). Le concept des ondes de plasma ioniques est moins connu que celui des ondes de plasma électroniques, mais il n'est pas nouveau, du moins pour les plasmas peu denses s1E. Nasser: "Fundamentals of gazeous ionization and plasma electronics", Wiley, 1971. s2F. F. Chen: "Introduction to plasma physics", Plenum Press, 1974. s3R.N. Franklin: "Plasma phenomena in gas discharges", Clarendon, Oxford, 1976..
Puisque ce concept pourrait devenir important pour l'étude du phénomène OVNI, il est utile de préciser nos idées, en nous limitant à l'essentiel. Considérons un plasma formé d'électrons et d'ions positifs. Supposons que les ions se déplacent seulement suivant une direction donnée, choisie comme axe des x. Le déplacement moyen d'un groupe d'ions positifs par rapport à sa position d'équilibre sera représenté par u = u(x,t). C'est une fonction de la position d'équilibre x et de l'instant t considéré. Pour trouver l'équation qui régit les variations possibles de u en fonction de x et de t, il faut tenir compte des densités des particules de charge positive ou négative, n± = n±(x,t). Dans son état d'équilibre, le plasma est électriquement neutre (n+ = n- = n), mais on peut rompre cet équilibre, en créant des oscillations collectives des ions positifs. Il en résulte un champ électrique oscillant, de grandeur E = E(x,t).
Pour aller plus loin, nous devons combiner 5 lois physiques :
- La loi de Gauss découle de la loi de Coulomb et relie les variations de E suivant l'axe des x aux différences entre n+ et n- à différents endroits.
- La densité n+ des ions positifs varie parce qu'il y a des ions qui sortent et d'autres qui entrent dans un volume donné. Il en découle que le changement de n+ par rapport à la densité à l'équilibre n dépend de la variation spatiale de u.
- Les électrons subissent beaucoup de collisions et se trouvent, en fait, dans un état d'équilibre thermique. La densité n- des électrons dépend alors de leur densité moyenne n, du potentiel électrique local V et de la température Te du système des électrons. Cela conduit à deux effets compétitifs, puisque la température Te traduit la tendance au désordre, mais les électrons tendent aussi à suivre les ions positifs. Etant chargés, les électrons subissent l'action du champ électrique E qui est défini par la variation locale du potentiel V.
- Il y a également des forces de pression, résultant des variations spatiales de la pression qui est définie par l'agitation thermique des ions et leur densité locale.
- La loi de Newton relie l'accélération moyenne des ions au champ électrique et aux forces de pression qu'ils subissent.
En combinant ces lois, on parvient à éliminer des variables, pour obtenir seulement une équation pour u(x,t) ou pour E(x,t). C'est l'équation des ondes de plasma ioniques. Elle démontre leur existence, comme les équations de Maxwell démontraient l'existence des ondes électromagnétiques. Elle définit en même temps leurs propriétés. Nous pouvons caractériser la variation spatiale par la longueur d'onde et la variation temporelle par la fréquence de l'onde, mais ces grandeurs sont liées entre elles, à cause de l'équation des ondes. Elle définit, en fait, la vitesse de propagation des ondes de plasma ioniques de fréquence ou de longueur d'onde donnée.
Les oscillations collectives des ions génèrent un champ électrique et celui-ci génère les oscillations ioniques. Les mouvements oscillatoires des ions et les oscillations du champ électrique sont inséparables et s'effectuent suivant la direction de propagation de l'onde. Ce sont des ondes longitudinales. La situation est très semblable pour les ondes acoustiques, mais dans ce cas, il n'y a pas de champ électrique. Notons que les ondes électromagnétiques sont transversales, parce que les champs électriques et magnétiques y oscillent perpendiculairement à la direction de propagation. Nous parlons par contre d'ondes électriques longitudinales.
Elles peuvent seulement exister dans un plasma, mais cela n'exclut pas l'air atmosphérique, partiellement ionisé. Dans ce cas, on doit perfectionner la théorie pour rendre compte de l'attachement des électrons et des collisions. J'ai commencé l'examen de ce types d'ondes, en cherchant à comprendre le phénomène de la "foudre en boule" s4F. Arago: "Sur le tonnère", Annuaire Bur. Longit. Paris, 1838 s5W. Brand: "Der Kugelblitz", Probleme der kosmischen Physik, Hamburg, 1923 s6S. Singer: "The nature of ball lightning", Plenum press, 1971 s7J.D. Barry: "Ball lightning and beadlightning, extreme forms of atmospheric electricity", Plenum press, 1980 s8W.N. Charman: "Ball lightning", Phys. Reports, 54, 261-306, 1979 s9B.M. Smirnov: "Physics of ball lightning" Phys. Reports, 224, 151-236 (1993) s10W. A. Corliss: "Handbook of unusual natural phenomena", 1978, 1982, 1993 s11M. Stenhoff: Ball lightning: an unsolved problem of atmospheric physics, 1999. Il s'agit également d'un plasma et d'oscillations ioniques, mais elles sont stationnaires au lieu d'être progressives.